Distortion implies a lack of similarities between reality and the image. Fisheye lenses produce images with extreme distortions that need exclusive software corrections based on different projection models and mapping functions.
Fisheye lenses are composed of several different lenses. During the imaging process, the incident light is refracted with different degrees and projected onto an imaging plane with a limited scale.
Fisheye projection model: Due to the multi-element structure of the fisheye lens assemblies, the analysis of the refraction relationship of the fisheye lenses becomes quite complicated, as shown in the figure below, a spherical projection model is proposed to illustrate the refraction relationship, this model decomposes the imaging process of the fisheye camera into two steps:

Figure 1. Fisheye projection
Step 1. Project three-dimensional space points onto a virtual unit sphere whose center coincides with the origin of the camera coordinate system.
Step 2. Projecting the points of the unit sphere onto the image plane. According to the different projection functions, the projection model can be further divided into the following table. (There is no single fisheye projection, but instead, there are a class of projection transformations all referred to as fisheye by various lens manufacturers, with names like equisolid angle projection, or equidistance fisheye. Less common are traditional spherical projections which map to circular images, such as the orthographic or stereographic projections.
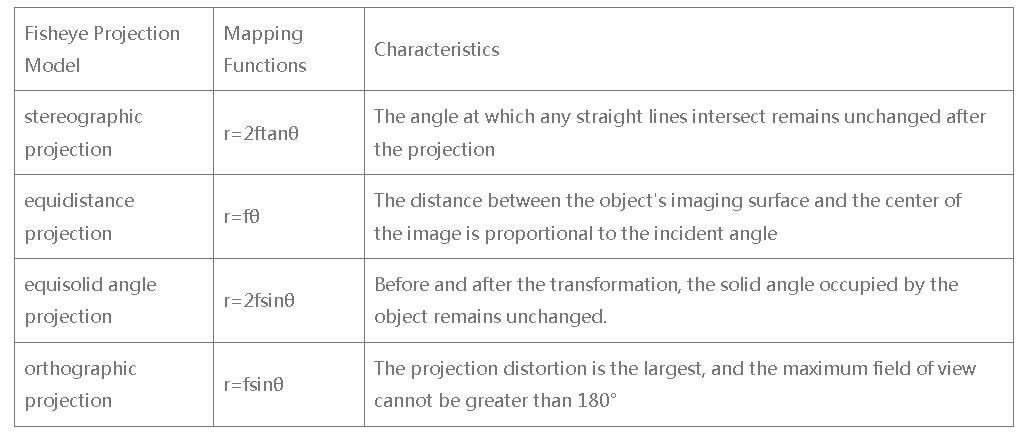
Note: for the mapping functions, f is the focal lengths of the fisheye lenses;θ is the angle between a point in the real world and the optical axis, which goes from the center of the image through the center of the lens; r is the radial position a point on the image on the film or sensor.
Below is a more detailed discussion of different types of fisheye projections:
1. Stereographic Projection
In comparison to other fisheye projections, the stereographic projection has the smallest distortion. The miniature surface elements on the spherical object surface will still be a small circle in the image after stereographic projection. Therefore, stereographic fisheye projection maintains high similarity in imaging small objects. However, it is this high similarity in imaging that makes this projection method unable to provide sufficient barrel distortion, shrinking the imaging field of view.
2. Equidistance Projection
The equidistant type fisheye lenses are the most prevalent type of fisheye lenses manufactured for cameras so far, especially when intended to be mapped into equirectangular images. These are also known as “tru-theta” or “f-theta” or what is regularly meant by a perfect fisheye mapping. The equidistant fisheye lenses are popular due to the appealing attribute that there is the same number of pixels per subtended angle on the periphery of the lens as the center. This fisheye projection model also has the advantage that its calculation is simpler relative to other fisheye projection models.
3. Equisolid Projection
As the name suggests, equisolid maintains an equal area for each pixel. That is, a pixel projected through the lens into the scene has the same solid angle irrespective of where on the lens it is.
4. Orthographic Projection
The magnification rates in the radial and tangential directions are different in orthogonal projection. When the field of view is 90°, the radial magnification rate is 0, that is, the edge image of the hemispherical object surface will form a straight line after being imaged using the orthogonal projection method.
Orthogonal projection can provide a greater amount of barrel distortion, which is more conducive to the expansion of the field of view. At the same time, the uniformity of the illumination distribution of the picture will be improved, but the orthogonal fisheye projection has few applications in practice.
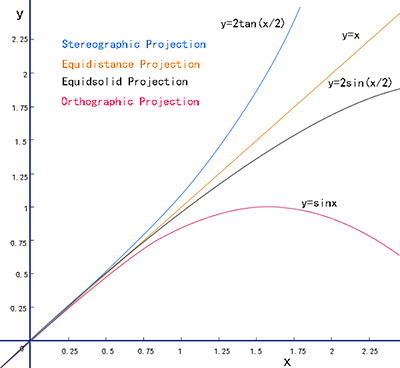
Figure 2. The mapping functions of the fisheye projection models

